Anchor Bolt Design

MecaStack performs anchor bolt designs for tensile and shear loads, using some common codes. This hasn’t always been true, starting in v5534 some new standards were added and this article explains the technical details associated with these new options. New design standards were added that the user can select and the stack was checked for the shear load at the base which had been ignored in prior versions.
Anchor Bolts per Brownell and Young
From the beginning of MecaStack (until v5532), the anchor bolt design was the same, which only checked the tensile capacity of the bolt. The baseplate design in MecaStack is based upon the book “Process Equipment Deisgn” by Brownell and Young. In this publication it recommended that the bolt area used be based upon the bolt “root area”, which is also sometimes referred to as the minor area. This is the most conservative area, which is based upon the minor diameter as shown below.
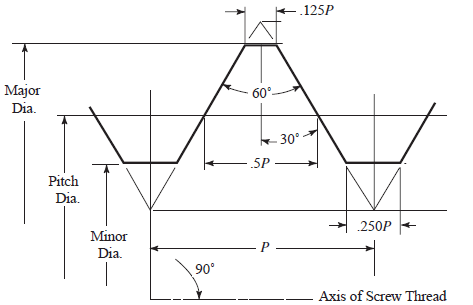
The allowable bolt tensile strength was based upon the AISC ‘Manual of Steel Construction’ 9th edition (Green book). This method was based upon Allowable Stress Design (ASD) and utilized Table J3.2. For LRFD (Strength Design) we increased this value by 1.5. The formulas used in MecaStack were as follows, where Fu is the Ultimate Tensile Stress of the Bolt material and Ab is the root area (minor area) of the bolt.
F_allow = 0.33 * Fu * Ab [ASD]
F_allow = 0.33 * 1.5 * Fu * Ab = 0.5 * Fu * Ab [LRFD]
Using the root area of the bolt and these allowable stress equations from the AISC 9th edition was conservative. This provided a much lower allowable load than can be obtained by modern methods. Please note that AISC 9th edition did not indicate that the root area must be used, this was just the conservative approach adopted in the early development of MecaStack, and it was never changed.
Shear Resistance:
The MecaStack anchor bolt design has never checked the stack for shear loads prior to v5534. The assumption has always been that the friction between the baseplate and foundation would be sufficient to resist the shear load at the base of the stack. In many cases, this assumption is true, but there are cases where it probably wasn’t true. In the cases where the friction is not sufficient, then the shear must be resisted by the anchor bolts since there is not an option to add a shear key to the baseplate. The baseplate holes are usually oversized, this introduces some complexity:
* The stack may slide before it engages any of the bolts
* All bolts may not be engaged at the same time
In an attempt to address these issues, MecaStack has taken the following approach:
1) The friction between baseplate and support is calculated. If it exceeds the applied shear, then no further checks are necessary. This friction is calculated using the dead weight and any pretension load that may be specified for the anchor bolts.
2) If the friction is not sufficient to resist the shear, then the shear above the friction resistance is determined. A calculation is made to determine how many anchor bolts are needed to resist the shear above the friction shear. If the number of bolts is less than 1/2 of the bolts provided, then the bolts are considered adequate to resist shear.
There are currently not any options in MecaStack to add a shear key to the baseplate; however, this is another method that could be followed to address high shear loads. The shear key design would need to be done manually outside of MecaStack.
American Concrete Institute 318-19:
Since most stacks are mounted on a concrete foundation, this standard is probably the best option for anchor bolt design for the majority of the stacks. The standard calculates the tensile and shear capacity separately, and there are not special provisions for combined tensile and shear as there are in some of the steel standards. The area is based upon the tensile area of the bolt. The calculations reduce to the following for ductile steel:
Tensile Capacity = 0.75*Ase*Futa {Eqn 17.6.1.2}
Cast-in Stud Anchors:
Shear Capacity* = 0.65*Ase*Futa {Eqn 17.7.1.2a}
Cast-In Hooked Anchors and Post-installed Anchors:
Shear Capacity* = 0.39*Ase*Futa {Eqn 17.7.1.2b}
Futa = Lessor of (Ult Tensile Strength, 1.9*Fy, 125 ksi [862.5 MPa])
Ase = Tensile Area of Bolt
* If a grout pad is used then multiply shear capacity by 0.8.
The above capacities are all based upon Strength Design (LRFD) and when we need to convert to an Allowable Stress Design (ASD) basis then we divide the above values by 1.5.

ACI Ductile Materials:
ACI 318-19 has different factors depending upon whether the material is ductile or brittle. In section 2.3, there is a definition of ductile steel that states that it’s ductile if the elongation is at least 14% and reduction in area is at least 30%. We have compiled a list of materials in MecaStack as well as these properties and have created the following table to determine which materials are considered ductile. Fortunately, most of the materials are defined as ductile and there are only a few that are considered brittle.

Canadian Standards Association A23.3:
The CSA A23.3 standard is also for concrete and is actually somewhat similar to the ACI 318-19. This standard has the similar differentiation of ductile versus brittle bolt materials. Although, CSA does define ductile as elongation of at least 14%, but there isn’t any mention of the reduction in area requirement as there was in ACI 318. For simplicity, we use the same brittle versus ductile criteria as we developed for ACI 318. For ductile anchor bolts, the following are the tensile and shear capacities:
Tensile Capacity = 0.68*Ase*Futa {Eqn D-3}
Cast-in Stud Anchors:
Shear Capacity* = 0.6375*Ase*Futa {Eqn D-20}
Cast-In Hooked Anchors and Post-installed Anchors:
Shear Capacity* = 0.3825*Ase*Futa {Eqn D-21}
Futa = Lessor of (Ult Tensile Strength, 1.9*Fy, 125 ksi [862.5 MPa])
Ase = Tensile Area of Bolt
* If a grout pad is used then multiply shear capacity by 0.8.
If load is seismic then all capacities multiplied by 0.75
All capacities are based upon Strength Design (LRFD) and if we desire Allowable Stress Design (ASD) then we divide these values by 1.5.

AISC 15th Edition, Section J3.6:
Using the 15th Edition of the AISC “Steel Construction Manual”, we can obtain much higher capacities than the older Brownell and Young method. The AISC equations are based upon using the area of the bolt ‘Ab’ based upon the nominal diameter of the bolt, rather than the root area; however, Fnt uses a factor of 0.75 which the commentary explains is an approximate conversion from the nominal area to the minor area. In addition, the factors used in the equations work out to be slightly higher than those used from the AISC 9th Edition.
Tensile:
Tensile Capacity = 0.375 * Fu * Ab {ASD Eqn J3-1}
Tensile Capacity = 0.5625 * Fu * Ab {LRFD Eqn J3-1}
Shear:
Shear Capacity = 0.225 * Fu * Ab {ASD Eqn J3-1}
Shear Capacity = 0.3375 * Fu * Ab {LRFD Eqn J3-1}

Combined Tensile & Shear:
When the anchor bolts are subjected to both Tensile and Shear loads we follow Section J3.7 to calculate the allowable bolt tension with consideration of the applied shear.
Fnt’ = 1.3*Fnt – ((2*Fnt)/Fnv)*fv <= Fnt {ASD Eqn J3-3a}
Fnt’ = 1.3*Fnt – (Fnt/(0.75*Fnv))*fv <= Fnt {LRFD Eqn J3-3b}
Fnt = Nominal Tensile Stress (0.75*Fu), Fnv = Nominal Shear Stress (0.45*Fu), ft = Actual Bolt Shear Stress
Adjusted Tensile Capacity = Fnt’ * Ab * (1/2) {ASD Eqn J3-2}
Adjusted Tensile Capacity = Fnt’ * Ab * 0.75 {LRFD Eqn J3-2}
Alternatively, we could solve this to find the allowable bolt shear with consideration of the applied tension.
Fnv’ = 1.3*Fnv – ((2*Fnv)/Fnt)*ft <= Fnv {ASD Eqn CJ3-7a}
Fnv’ = 1.3*Fnv – (Fnv/(0.75*Fnt))*ft <= Fnv {LRFD Eqn CJ3-7b}
Adjusted Shear Capacity = Fnv’ * Ab * (1/2) {ASD Eqn J3-2}
Adjusted Shear Capacity = Fnv * Ab * 0.75 {LRFD Eqn J3-2}
Canadian S16 ‘Limit States Design of Steel Structures’:
Similar to the AISC method, the equations in S16 Clause 13.12.1.3 are also based upon using the nominal area of the bolt. Simplifying the equations provided in the manual and using the phi value for anchor rods (0.67), they become the following:
Tensile Capacity = 0.5025 * Fu * Ab {Cl 13.12.1.2}
Shear Capacity = 0.2814 * Fu * Ab {Cl 13.12.1.1 Anchor Rods}
When combined tensile and shear are applied, we must check interaction:
(Tensile / Tensile Capacity)^2 + (Shear / Shear Capacity)^2 <= 1
{Cl 13.12.1.3}
Please note that the Canadian standard is based upon limit state design and we divide by 1.5 to get an approximate bolt strength for Allowable Stress Design (ASD).

British ‘Steel Building Design Data’:
We have incorporated the British publication ‘Steel building Design Data’ for the evaluation of the anchor bolts. These equations reduce to the following:
Tensile Capacity = 0.72 * Fu * As {Cl 11.1}
Shear Capacity = 0.48 * Fu * As {Cl 11.1}
As = Tensile Area of Bolts
Fu = Ultimate Tensile Stress
This publication is based upon Strength Design (LRFD) and when we desire Allowable Stress Design (ASD) we divide these capacities by 1.5.

MecaStack Anchor Bolt Tensile Strength:
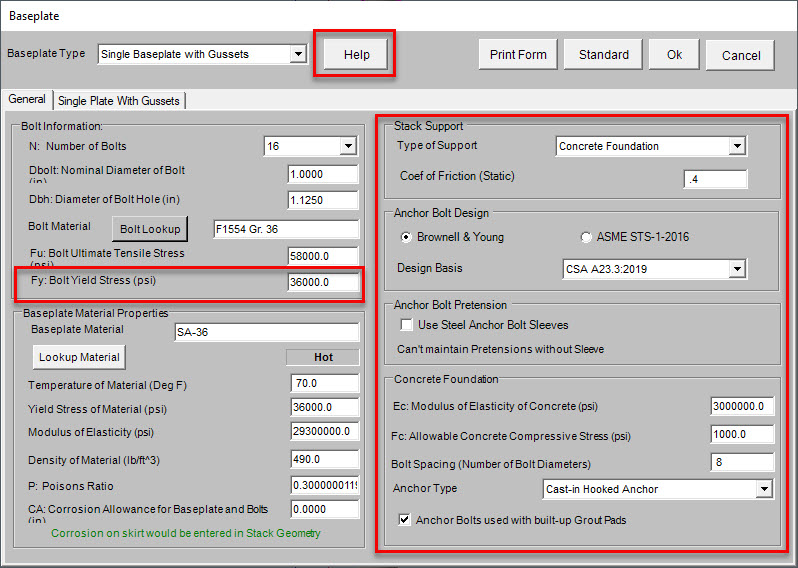
MecaStack v5534 incorporated some major changes with regard to the design of anchor bolts. As of v5534, the software now checks the shear load acting on the base of the structure and verifies that there is adequate shear resistance. This is true for all of the bases except the Brownell and Young. We have left it as-is so that users can replicate legacy files to match past results. At the time this article was written, v5534 was the most recent release, and here are the major changes made:
1) Yield stress added since it’s needed for ACI 318 and CSA A23.3
2) Specify whether support is concrete or steel. If it’s steel, then it defaults to the STS method for the tension calculation, and all support properties are defaulted to match the baseplate.
3) Coefficient of Friction is now entered, which is used to check the shear resistance of the base.
4) Several parameters added with regard to the anchor bolt design that are needed if ACI 318 or CSA A23.3 are specified (Anchor Type, Grout Pad, Pretension).
5) A help button added that provides immediate help on the fields contained on this form.
6) On baseplate material properties, we only use Hot properties now since the Cold were not being used anywhere.
Pretension was added, but this will be a topic of a separate article.
Comparison of Methods:
A comparison of the methods to check anchor bolt tensile strength, shows that the old Brownell and Young method is by far the most conservative. Based upon a 2 in [50 mm] anchor bolt, F1554 Gr. 36, the tensile and shear capacity was calculated for each design standard. If the friction is not sufficient to resist the shear load, then the combined effects of tension and shear must be checked for the steel design codes (AISC 15th Ed, CSA S16 and British); however, for simplicity we have assumed that friction is sufficient to resist the shear loads and provided the full shear capacity of the bolts. The concrete codes assume NO grout pad has been used (using a grout pad reduces shear capacity by 20%) and that we are using Hooked anchors.
Below is a summary of all of the capacities for each standard. It can be seen that Brownell and Young (legacy method within MecaStack) produces by far the lowest Ultimate Tensile capacity. The other tensile capacities range from a low of 395 KN to a high of 466 KN, thus the highest capacity is about 18% higher than the lowest. The shear capacities range from a low of 221 KN to a high of 299 KN, thus the highest is about 35% higher than the lowest. These results for shear capacity are more scattered for a variety of reasons. The concrete codes are based upon hooked anchor bolts, while the steel codes don’t make any distinction in hooked versus stud bolts. If we had a grout pad, then the concrete shear capacities would have been 20% lower than those shown below.
| Standard | Ultimate Tensile Capacity (KN) |
Ultimate Shear Capacity (KN) |
| ACI 318-19 | 466 | 243 |
| CSA A23.3 | 423 | 238 |
| AISC 15th Ed | 442 | 265 |
| CSA S16 | 395 | 221 |
| British | 448 | 299 |
| Brownell & Young | 307 | N/A |
Conclusions:
If the stack is supported on a concrete foundation then the best code to be utilized is either ACI 318 or CSA A23.3, since those codes are conservative and relate specifically to anchor bolt design for a concrete foundation. MecaStack checks the anchor rods for tension and shear only, all other checks must be performed by the foundation designer.
If a stack is mounted on a steel frame, then one of the steel codes would be most appropriate. These consist of AISC 15th Ed, CSA S16 and British.
The Brownell and Young Method is included for legacy files, but although it is conservative with regard to tensile capacities it is deficient in that it doesn’t verify the shear capacity.
