I Feel the Need to Change Wind Speed

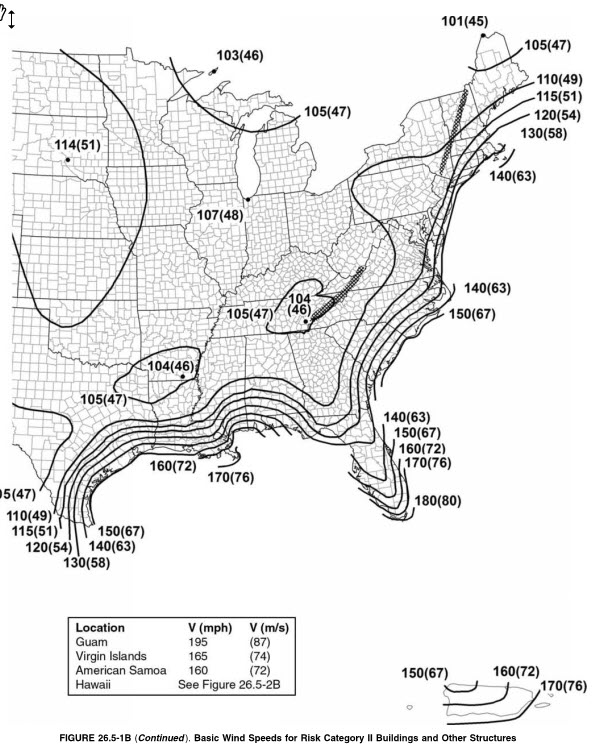
It was Tom Cruise in “Top Gun” who once said, “I feel the need, the need for speed”.  I sometimes wonder if Tom Cruise is on the ASCE 7 committee, because it feels like they have the need to change the wind speed basis with every new release of ASCE 7.  I’m not complaining, because this change is good for the wind software business; however, it does create a lot of confusion.   For example, I live in Broken Arrow, Oklahoma, and for a category II structure the ASCE 7-05 standard indicated we should design to a wind speed of 90 mph.  Then in ASCE 7-10 and ASCE 7-16, the same category II structure needs to be designed for 107 mph.  That’s a fairly significant increase, or is it?  

The Basics:

First we need to get back to basics and determine the basic parameters ASCE 7 uses to determine wind speeds.  Here are the basic parameters you need to know in addition to wind speed.

Reference Elevation – Wind speed increases at higher elevation, and so we need to know at what elevation the wind speed is measured. ASCE 7 uses a reference elevation of 33 ft [10 m].

Gust Duration – If we measure wind speed averaged over a 3 second time frame, we would expect a higher wind speed than we would if the wind speed were averaged over 60 seconds. Fortunately, all versions of ASCE 7 use a 3 second gust basis, but other codes around the world use different values.

Recurrence/Probability – If we found the worst wind to occur in a 50 year period, then we would expect the wind speed to be less than if it were a wind speed in a 1,000 year period; therefore, we need to know over what period of time that a wind speed can occur. This is also referred to as the probability that a wind speed can occur in X years.

If you put all of these parameters together, then this would be the summary of the parameters for ASCE 7 codes:

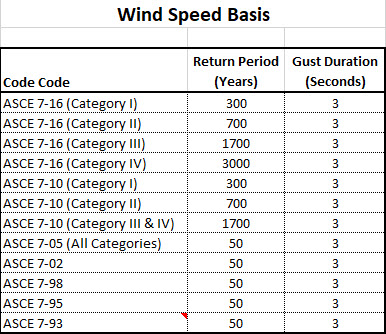
The first notable thing is that in ASCE 7-05 and earlier, there is only one return period for the entire standard.  Starting in ASCE 7-10 and later versions, there is a different return period for each category.   

In ASCE 7-05 and earlier, we used a single wind speed for a single location, and then we accounted for the “structural category” by using importance factors.  For example, if it was an essential building such as a hospital then we would use Category IV, and then the importance factor would be 1.15.  This would multiply the wind velocity by 1.15, and would significantly increase the wind loads. 

Starting in ASCE 7-10, there were different wind maps for each structural category.  The importance factor was eliminated and the higher categories used a higher wind speed than the lower categories.   If we are looking up a wind speed for a location, we must also know the category of the structure, because the wind maps change for each category.   

Ultimate Wind Speeds:

The wind speeds in ASCE 7-10 and later are considered “Ultimate” wind speeds, where as the wind speeds in ASCE 7-05 and earlier are Allowable Stress Design (ASD) wind speeds.  The Ultimate indicates that the wind pressures calculated are to be used with the Ultimate (Strength) load combinations provided in ASCE 7-16 Sec 2.3, whereas in ASCE 7-05 we used the wind pressures in the Allowable Stress Design (ASD) combinations.  This can all become a little confusing, and so we have worked an example in this document to illustrate.  In this example, I use the same wind speeds that I mentioned at the begining of this article.  This shows that even though we used 90 mph with ASCE 7-05 and 115 mph with ASCE 7-10, that the final pressures are actually quite similar when we take all other factors into consideration.  There are areas of the US (Typically along the coasts) where the pressures won’t match so closely, but in much of the US both codes (ASCE 7-05 and ASCE 7-10) will give similar results if applied correctly.  

Free Wind Speed Conversion Tool:

 If you are using ASCE 7 for design, then you simply look up your location in the latest version to determine what wind speed to use for design.  There are instances where you may be trying to convert from a wind speed provided in another country to that of ASCE 7, or vice versa.  In these instances we have created a free wind conversion tool to help with that conversion from one code to another.  To receive it, you simply need to sign up for our newsletter, and one of the emails in that welcome sequence of emails provides the link to download this free tool.