Getting High on Wind

I am an amateur cyclist, and I typically ride my bike on trails in my home of Broken Arrow, Oklahoma at an elevation of 700 ft [213 m]. One year I took my bike on a vacation to Breckenridge, Colorado at an elevation of 9,000 ft [2743 m]. The first thing I noticed when riding in Breckenridge was that there was a significant decrease in oxygen. The second thing I noticed was that the wind resistance was significantly less when I was pedaling into a headwind than it would have been in Oklahoma. This was due to the density of air being less, and therefore the wind resistance was reduced.
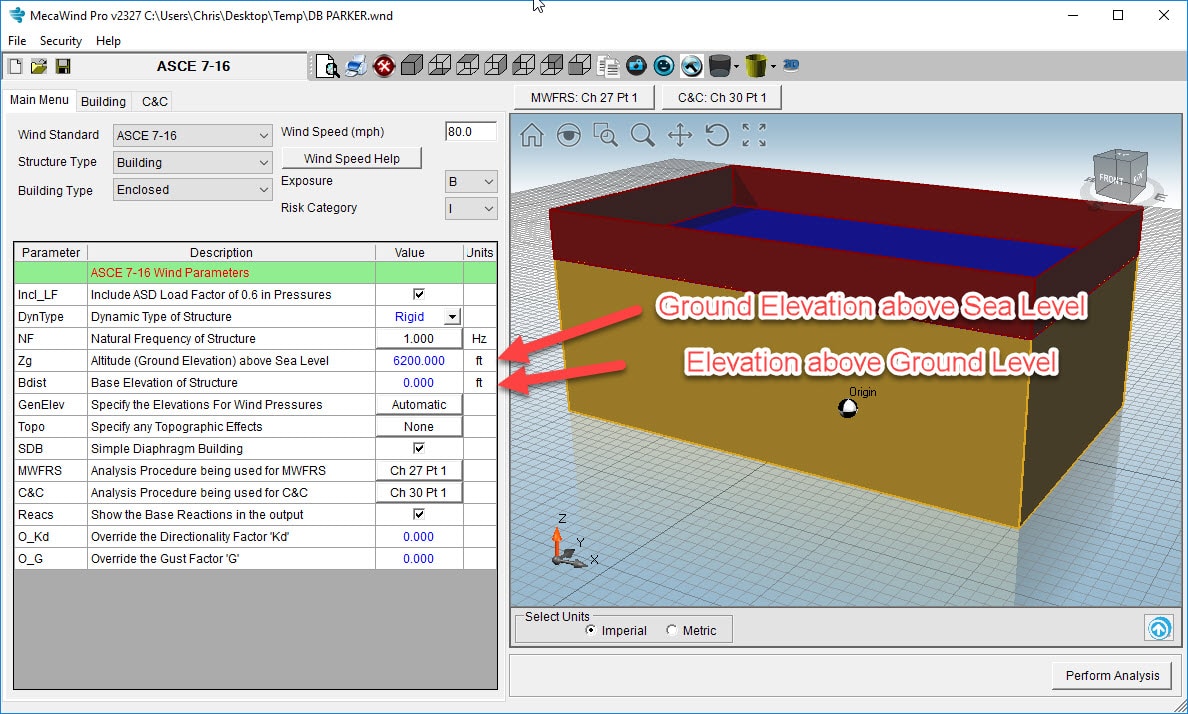
When calculating wind pressures per ASCE 7-16 there is a new consideration, that allows you to consider lower wind pressures due to the thinner air at high altitudes. This is not to be mistaken with the elevation above grade. Since this has been the source of some confusion, I wanted to explain the difference.
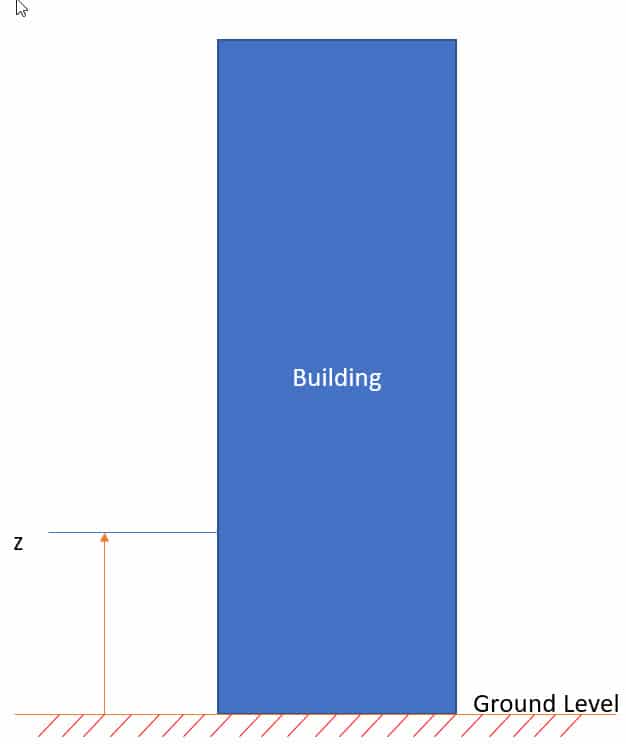
Elevation Above Ground Level, z:
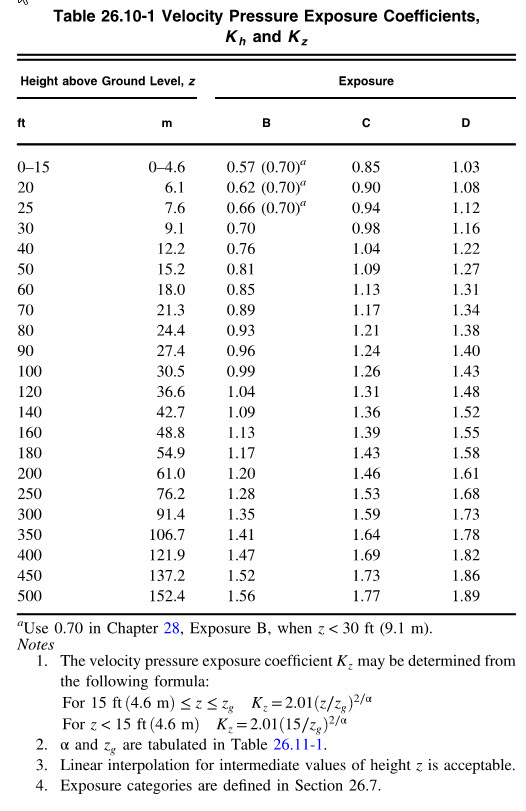
The height above ground level has always been a consideration in wind pressure calculations. This is referring to the elevation above ground level. At ground level, there are many obstructions (buildings, trees, terrain, etc.) that slow down the wind, and at very high elevations above grade there is nothing interferring with the wind. It makes sense that as the elevation above ground increases, so does the wind velocity. This is accounted for in the ASCE 7 standard by use of the “Kz” and “Kh” factors. Referring to Table 26.10-1, the “Kz” factor is dependent upon the exposure, and gets larger as the elevation increases. The exposure is a consideration because at exposure B there are more ground level obstructions than there would be at exposures C and D.

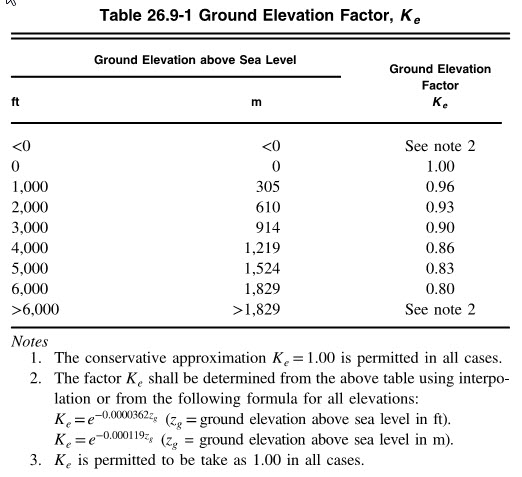
Elevation above Sea Level:
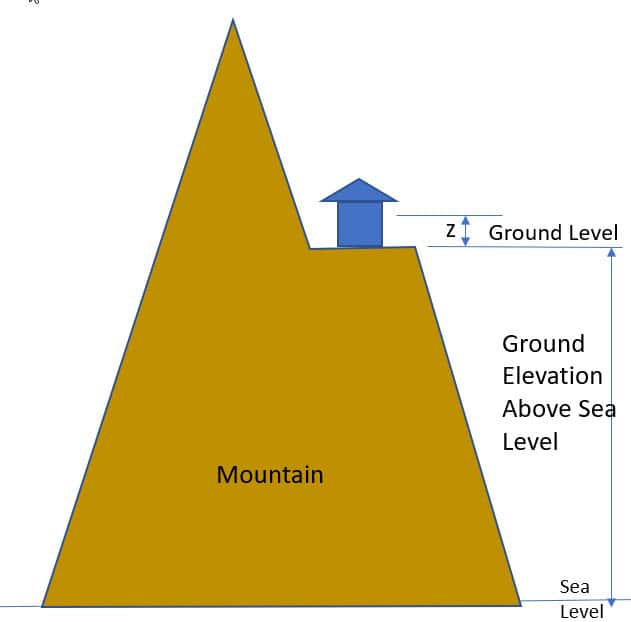
In the 2016 version of ASCE 7, a new parameter was introduced, Ground Elevation Factor “Ke”. This parameter is dependent upon the ground elevation above sea level. As seen in Table 26.9-1, the “Ke” decreases as the altitude increases. The theory here is that the wind pressure is based on the density of air, and as the density decreases, the pressure also decreases. If we have the same wind velocity, then we can see from Table 26.9-1 that the wind pressure at a site that is 6,000 ft [1829 m] above sea level will be 80% of the pressure calculated for the same wind speed at sea level. This is a significant decrease. As seen in the illustration below, the ground level then becomes the local ground level for the structure. Then the “Kz”/”Kh” factors are calculated just as they were before, but z is measured from the local “ground level” up to the area of interest.
Is Ke really new?
Did you know that the versions of ASCE 7 prior to 2016 actually had provisions to account for altitude above sea level, but they were back in the commentary. In Paragraph C27.3.2 of ASCE 7-10, the constant of 0.00256 (or 0.613 in SI) in the pressure calculation, was based upon the mass density of air at sea level. There was then a table for the density of air at various altitudes, and a method to calculate a new constant to be used. Here is a sample calculation for the constant at an elevation of 0 ft (sea level) and 6,000 ft [1829 m] above sea level.
0 ft [0 m] Average Air Density = 0.0765 lb/ft^3
Constant = 0.5*[(0.0765 lb/ft^3)/(32.2 ft/s^2)]*[(5280 ft/mi)*(1 hr/3600 sec)]^2 = 0.00256
6,000 ft [1829 m] Average Air Density = 0.0639 lb/ft^3
Constant = 0.5*[(0.0639 lb/ft^3)/(32.2 ft/s^2)]*[(5280 ft/mi)*(1 hr/3600 sec)]^2 = 0.00214
If you ratio 0.00214 / 0.00256 you get 0.835. If you will note that the Ke factor at 6000 ft from Table 26.9-1 is 0.8, so the two are in the same range.
The wind pressure equation is as follows:
qz = 0.00256 * Kz * Kzt * Kd * V^2 {ASCE 7-10, Eqn 27.3-1}
Considering the altitude, it is then modified to be:
qz = (Constant) * Kz * Kzt * Kd * V^2
Conclusion:
The ASCE 7-16 (and previous releases) do give provisions to reduce the wind pressure to account for the air being less dense at higher altitudes. I can’t say that I have personally taken this reduction in my designs of equipment, because I prefer to stay conservative and use Ke = 1; however, it is a legitimite reduction that could play a major benefit for very tall structures.
In our MecaWind software, the entry of each value is shown below. Once entered correctly, the software will calculate Kz and Ke automatically, and the designer doesn’t need to do anything else.